Embedded 嵌入法

Embedded（嵌入法）是特征选择的一种方法，它先使用某些机器学习的算法和模型进行训练，得到各个特征的权值系数，根据系数从大到小选择特征。这种方法通过训练来确定特征的优劣。

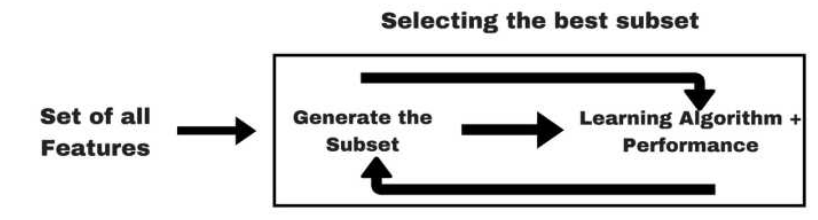
基于线性模型的Embedded

下面将介绍如何用线性模型的系数来选择特征。越是重要的特征在模型中对应的系数就会越大，而跟输出变量越是无关的特征对应的系数就会越接近于0。在噪音不多的数据上，或者是数据量远远大于特征数的数据上，如果特征之间相对来说是比较独立的，那么即便是运用最简单的线性回归模型也一样能取得非常好的效果。

正则化

正则化就是把额外的约束或者惩罚项加到已有模型（损失函数）上，以防止过拟合并提高泛化能力。损失函数由原来的 $L(X,Y)$ 变为 $L(X,Y)+\alpha \left| w \right|$ ， $w$ 是模型系数组成的向量（有些地方也叫参数parameter，coefficients）， $\left\| \cdot \right\|$ 一般是L1或者L2范数， $\alpha$ 是一个可调的参数，控制着正则化的强度。当用在线性模型上时，L1正则化和L2正则化也称为Lasso(least absolute shrinkage and selection operator)和Ridge。使用带惩罚项的基模型，除了筛选出特征外，同时也进行了降维。

L1正则化(Lasso)

L1正则化将系数 $w$ 的L1范数作为惩罚项加到损失函数上，由于正则项非零，这就迫使那些弱的特征所对应的系数变成0。因此L1正则化往往会使学到的模型很稀疏（系数w经常为0），这个特性使得L1正则化成为一种很好的特征选择方法。

Scikit-learn为线性回归模型提供了Lasso，为分类模型提供了L1逻辑回归。下面的例子在波士顿房价数据上运行了Lasso，其中参数 $\alpha$ 是通过gird search进行优化的。

from sklearn.linear_model import Lasso
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import load_boston
import numpy as np

boston = load_boston()
scaler = StandardScaler()
X = scaler.fit_transform(boston["data"])
Y = boston["target"]
names = boston["feature_names"]

lasso = Lasso(alpha=.3)
lasso.fit(X, Y)
print("Lasso model: ", pretty_print_linear(lasso.coef_, names, sort=True))

输出为，

Lasso model: -3.707 * LSTAT + 2.992 * RM + -1.757 * PTRATIO + -1.081 * DIS + -0.7 * NOX + 0.631 * B + 0.54 * CHAS + -0.236 * CRIM + 0.081 * ZN + -0.0 * INDUS + -0.0 * AGE + 0.0 * RAD + -0.0 * TAX

可以看到，很多特征的系数都是0。如果继续增加 $\alpha$ 的值，得到的模型就会越来越稀疏，即越来越多的特征系数会变成0。

然而，L1正则化像非正则化线性模型一样也是不稳定的，如果特征集合中具有相关联的特征，当数据发生细微变化时也有可能导致很大的模型差异。

当希望减少特征的维度以用于其它分类器时，可以通过 feature_selection.SelectFromModel 来选择不为0的系数。sklearn特别指出，常用于此目的的稀疏预测模型有 linear_model.Lasso （回归）， linear_model.LogisticRegression 和 svm.LinearSVC （分类）:

>>> from sklearn.svm import LinearSVC
>>> from sklearn.datasets import load_iris
>>> from sklearn.feature_selection import SelectFromModel
>>> iris = load_iris()
>>> X, y = iris.data, iris.target
>>> X.shape
(150, 4)
>>> lsvc = LinearSVC(C=0.01, penalty="l1", dual=False).fit(X, y)
>>> model = SelectFromModel(lsvc, prefit=True)
>>> X_new = model.transform(X)
>>> X_new.shape
(150, 3)

使用feature_selection库的SelectFromModel类结合带L1惩罚项的逻辑回归模型，来选择特征的代码如下：

from sklearn.feature_selection import SelectFromModel
from sklearn.linear_model import LogisticRegression

#带L1惩罚项的逻辑回归作为基模型的特征选择
SelectFromModel(LogisticRegression(penalty="l1", C=0.1)).fit_transform(iris.data, iris.target)

L2正则化(Ridge Regression)

L2正则化同样将系数向量的L2范数添加到了损失函数中。由于L2惩罚项中系数是二次方的，这使得L2和L1有着诸多差异，最明显的一点就是，L2正则化会让系数的取值变得平均。对于关联特征，这意味着他们能够获得更相近的对应系数。还是以 $Y=X_1+X_2$ 为例，假设 $X_1$ 和 $X_2$ 具有很强的关联，如果用L1正则化，不论学到的模型是 $Y=X_1+X_2$ 还是 $Y=2X_1$ ，惩罚都是一样的，都是 $2\alpha$ 。但是对于L2来说，第一个模型的惩罚项是 $2\alpha$ ，但第二个模型的是 $4\alpha$ 。可以看出，系数(待求参数)之和为常数时，各系数相等时惩罚是最小的，所以才有了L2会让各个系数趋于相同的特点。

可以看出，L2正则化对于特征选择来说一种稳定的模型，不像L1正则化那样，系数会因为细微的数据变化而波动。所以L2正则化和L1正则化提供的价值是不同的，L2正则化对于特征理解来说更加有用：表示能力强的特征对应的系数是非零。

回过头来看看3个互相关联的特征的例子，分别以5个不同的种子随机初始化运行5次，来观察L1和L2正则化的稳定性。

import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn.linear_model import Ridge

size = 100
# We run the method 5 times with different random seeds
for i in range(5):
    print("Random seed %s" % i)
    np.random.seed(seed=i)
    X_seed = np.random.normal(0, 1, size)
    X1 = X_seed + np.random.normal(0, .1, size)
    X2 = X_seed + np.random.normal(0, .1, size)
    X3 = X_seed + np.random.normal(0, .1, size)
    Y = X1 + X2 + X3 + np.random.normal(0, 1, size)
    X = np.array([X1, X2, X3]).T
    lr = LinearRegression()
    lr.fit(X, Y)
    print("Linear model:", pretty_print_linear(lr.coef_))
    ridge = Ridge(alpha=10)
    ridge.fit(X, Y)
    print("Ridge model:", pretty_print_linear(ridge.coef_))
    print()

输出为，

Random seed 0
Linear model: 0.728 * X0 + 2.309 * X1 + -0.082 * X2
Ridge model: 0.938 * X0 + 1.059 * X1 + 0.877 * X2

Random seed 1
Linear model: 1.152 * X0 + 2.366 * X1 + -0.599 * X2
Ridge model: 0.984 * X0 + 1.068 * X1 + 0.759 * X2

Random seed 2
Linear model: 0.697 * X0 + 0.322 * X1 + 2.086 * X2
Ridge model: 0.972 * X0 + 0.943 * X1 + 1.085 * X2

Random seed 3
Linear model: 0.287 * X0 + 1.254 * X1 + 1.491 * X2
Ridge model: 0.919 * X0 + 1.005 * X1 + 1.033 * X2

Random seed 4
Linear model: 0.187 * X0 + 0.772 * X1 + 2.189 * X2
Ridge model: 0.964 * X0 + 0.982 * X1 + 1.098 * X2

可以看出，不同的数据上线性回归得到的模型（系数）相差甚远，但对于L2正则化模型来说，结果中的系数非常的稳定，差别较小，都比较接近于1，能够反映出数据的内在结构。

基于树模型的Embedded

基于树的预测模型能够用来计算特征的重要程度，因此能根据特征的重要性用来去除无关紧要的特征。

sklearn导入树模块计算特征的重要程度，然后结合sklearn.feature_selection.SelectFromModel 去除不相关特征：

>>> from sklearn.ensemble import ExtraTreesClassifier
>>> from sklearn.datasets import load_iris
>>> from sklearn.feature_selection import SelectFromModel
>>> iris = load_iris()
>>> X, y = iris.data, iris.target
>>> X.shape
(150, 4)
>>> clf = ExtraTreesClassifier()
>>> clf = clf.fit(X, y)
>>> clf.feature_importances_  
array([ 0.04...,  0.05...,  0.4...,  0.4...])
>>> model = SelectFromModel(clf, prefit=True)
>>> X_new = model.transform(X)
>>> X_new.shape               
(150, 2)

树模型中GBDT也可用来作为基模型进行特征选择，使用feature_selection库的SelectFromModel类结合GBDT模型，来选择特征的代码如下：

from sklearn.feature_selection import SelectFromModel
from sklearn.ensemble import GradientBoostingClassifier

#GBDT作为基模型的特征选择
SelectFromModel(GradientBoostingClassifier()).fit_transform(iris.data, iris.target)

随机森林具有准确率高、鲁棒性好、易于使用等优点，这使得它成为了目前最流行的机器学习算法之一。随机森林提供了两种特征选择的方法：平均不纯度减少(mean decrease impurity) 和平均精确率减少(mean decrease accuracy)。

平均不纯度减少(mean decrease impurity)

随机森林由多个决策树构成。决策树中的每一个节点都是关于某个特征的条件，为的是将数据集按照不同的响应变量一分为二。利用不纯度可以确定节点（最优条件），对于分类问题，通常采用 基尼不纯度 或者 信息增益 ，对于回归问题，通常采用的是方差或者 最小二乘拟合。当训练决策树的时候，可以计算出每个特征减少了多少树的不纯度。对于一个决策树森林来说，可以算出每个特征平均减少了多少不纯度，并把它平均减少的不纯度作为特征选择的值。

下面的例子是sklearn中基于随机森林的特征重要度度量方法：

from sklearn.datasets import load_boston
from sklearn.ensemble import RandomForestRegressor
import numpy as np

#Load boston housing dataset as an example
boston = load_boston()
X = boston["data"]
Y = boston["target"]
names = boston["feature_names"]
rf = RandomForestRegressor()
rf.fit(X, Y)
print("Features sorted by their score:")
print(sorted(zip(map(lambda x: "%.4f"%x, rf.feature_importances_), names), reverse=True))

这里特征得分采用的是 Gini Importance。输出为：

Features sorted by their score:
[('0.5128', 'LSTAT'), ('0.2896', 'RM'), ('0.0792', 'DIS'), ('0.0311', 'CRIM'), ('0.0188', 'NOX'), ('0.0179', 'AGE'), ('0.0174', 'TAX'), ('0.0123', 'PTRATIO'), ('0.0086', 'B'), ('0.0074', 'RAD'), ('0.0037', 'INDUS'), ('0.0007', 'ZN'), ('0.0007', 'CHAS')]

平均精确率减少(mean decrease accuracy)

另一种常用的特征选择方法就是直接度量每个特征对模型精确率的影响。主要思路是打乱每个特征的特征值顺序，并且度量顺序变动对模型的精确率的影响。很明显，对于不重要的变量来说，打乱顺序对模型的精确率影响不会太大，但是对于重要的变量来说，打乱顺序就会降低模型的精确率。

这个方法sklearn中没有直接提供，但是很容易实现，下面继续在波士顿房价数据集上进行实现。

from sklearn.cross_validation import ShuffleSplit
from sklearn.metrics import r2_score
from sklearn.datasets import load_boston
from collections import defaultdict
from sklearn.ensemble import RandomForestRegressor
import numpy as np

boston = load_boston()
X = boston["data"]
Y = boston["target"]
names = boston["feature_names"]

rf = RandomForestRegressor()
scores = defaultdict(list)
# crossvalidate the scores on a number of different random splits of the data
for train_idx, test_idx in ShuffleSplit(len(X), 100, .3):
    X_train, X_test = X[train_idx], X[test_idx]
    Y_train, Y_test = Y[train_idx], Y[test_idx]
    r = rf.fit(X_train, Y_train)
    acc = r2_score(Y_test, rf.predict(X_test))
    for i in range(X.shape[1]):
        X_t = X_test.copy()
        np.random.shuffle(X_t[:, i])
        shuff_acc = r2_score(Y_test, rf.predict(X_t))
        scores[names[i]].append((acc - shuff_acc) / acc)
print("Features sorted by their score:")
print(sorted( [(float('%.4f'%np.mean(score)), feat) for
              feat, score in scores.items()], reverse=True) )

输出为：

Features sorted by their score:
[(0.7508, 'LSTAT'), (0.5691, 'RM'), (0.0947, 'DIS'), (0.0396, 'CRIM'), (0.0371, 'NOX'), (0.0223, 'PTRATIO'), (0.0173, 'TAX'), (0.0132, 'AGE'), (0.0071, 'B'), (0.0053, 'INDUS'), (0.0036, 'RAD'), (0.0005, 'CHAS'), (0.0003, 'ZN')]

在这个例子当中，LSTAT和RM这两个特征对模型的性能有着很大的影响，打乱这两个特征的特征值使得模型的性能下降了75%和57%。注意，尽管这些我们是在所有特征上进行了训练得到了模型，然后才得到了每个特征的重要性测试，这并不意味着我们扔掉某个或者某些重要特征后模型的性能就一定会下降很多，因为即便某个特征删掉之后，其关联特征一样可以发挥作用，让模型性能基本上不变。

最大熵模型MaxEnt

最大熵原理

MaxEnt 是概率模型学习中一个准则，其思想为：在学习概率模型时，所有可能的模型中熵最大的模型是最好的模型；若概率模型需要满足一些约束，则最大熵原理就是在满足已知约束的条件集合中选择熵最大模型。最大熵原理指出，对一个随机事件的概率分布进行预测时，预测应当满足全部已知的约束，而对未知的情况不要做任何主观假设。在这种情况下，概率分布最均匀，预测的风险最小，因此得到的概率分布的熵是最大。

最大熵模型简介

接下来以统计建模的形式来描述 MaxEnt 模型，给定训练数据 ${(x_i,y_i)_{i=1}^N}$ ，现在要通过最大熵来建立一个概率判别模型，该模型的任务是对于给定的 $X=x$以条件概率分布 $P(Y|X=x)$ 预测 $Y$ 的取值。根据训练语料能得出 $(X,Y)$ 的经验分布，得出部分 $(X,Y)$ 的概率值，或某些概率需要满足的条件,即问题变成求部分信息下的最大熵或满足一定约束的最优解，约束条件是靠特征函数来引入的。

特征函数

特征函数 $f(x,y)$ 描述 $x$ 与 $y$ 之间的某一事实，其定义如下：

$f(x,y) = \left \{ \begin{aligned} 1, & \ 当 \ x、y \ 满足某一事实.\\ 0, & \ 不满足该事实.\\ \end{aligned}\right .$

特征函数 $f(x,y)$ 是一个二值函数，当 $x$ 与 $y$ 满足事实时取值为 1 ，否则取值为 0。

约束条件

接下来看经验分布，现在把训练数据当做由随机变量 $(X,Y)$ 产生,则可以根据训练数据确定联合分布的经验分布 $\widetilde{P}(X,Y)$ 与边缘分布的经验分布 $\widetilde{P}(X)$ :

$\begin{aligned} \widetilde{P}(X = x,Y = y) &= \frac{count(X=x,Y= y)}{N}\\ \widetilde{P}(X = x) &= \frac{count(X=x)}{N} \end{aligned}$

用 $E _{\widetilde{P}}(f)$ 表示特征函数 $f(x,y)$ 关于经验分布 $\widetilde{P}(X ,Y )$ 的期望，可得：

$E _{\widetilde{P}}(f) = \sum_{x,y}\widetilde{P}(x ,y)f(x,y) = \frac{1}{N} \sum_{x,y}f(x,y)$

$\widetilde{P}(X,Y)$ 前面已经得到了，数数 $f(x,y)$ 的次数就可以了，由于特征函数是对建立概率模型有益的特征，所以应该让 MaxEnt 模型来满足这一约束，所以模型 $P(Y|X)$ 关于函数 $f$ 的期望应该等于经验分布关于 $f$ 的期望，模型 $P(Y|X)$ 关于 $f$ 的期望为：

$E_P(f) =\sum_{x,y}P(x,y)f(x,y) \approx \sum_{x,y}\widetilde{P}(x)P(y|x)f(x,y)$

经验分布与特征函数结合便能代表概率模型需要满足的约束，只需使得两个期望项相等，即 $E_P(f) = E _{\widetilde{P}}(f)$ :

$\sum_{x,y}\widetilde{P}(x)p(y|x)f(x,y) = \sum_{x,y}\widetilde{P}(x ,y)f(x,y)$

上式便为 MaxEnt 中需要满足的约束，给定 $n$ 个特征函数 $f_i(x,y)$ , 则有 $n$ 个约束条件，用 $C$ 表示满足约束的模型集合：

$C = \left\{ P \ | \ E_P(f_i) = E _{\widetilde{P}}(f_i) ,I = 1,2,…,n \right \}$

从满足约束的模型集合 $C$ 中找到使得 $P(Y|X)$ 的熵最大的即为 MaxEnt 模型了。

最大熵模型目标函数

关于条件分布 $P(Y|X)P(Y|X)$ 的熵为：

$H(P)=–∑x,yP(y,x)logP(y|x)=–∑x,y\widetilde{P}(x)P(y|x)logP(y|x)$

首先满足约束条件然后使得该熵最大即可，MaxEnt 模型 $P^*$ 为：

$P^∗=argmax_{P∈C}H(P)$ 或 $P^∗=argmin_{P∈C}-H(P)$

综上给出形式化的最大熵模型，

给定数据集 ${(x_i,y_i)_{i=1}^N}$ ，特征函数 $f_i(x,y)$ ， $i=1,2…,n$ ，根据经验分布得到满足约束集的模型集合 $C$ ：

$min_{P \in C} \sum_{x,y}\widetilde{P}(x)P(y|x)logP(y|x)$

$s.t. E_p(f_i)=E_{\widetilde{P}}(f_i)$

$\sum_yP(y|x)=1$

最大熵模型被形式化为带有约束条件的最优化问题之后，可以通过拉格朗日乘子法将其转为无约束优化的问题，然后进一步求解。

深度学习中的特征选择

深度学习能够自动进行特征的提取与选择。

深度学习与传统模式识别方法的最大不同在于它是从大数据中自动学习特征，而非采用手工设计的特征。好的特征可以极大提高模式识别系统的性能。在过去几十年模式识别的各种应用中，手工设计的特征处于同统治地位。它主要依靠设计者的先验知识，很难利用大数据的优势。由于依赖手工调参数，特征的设计中只允许出现少量的参数。深度学习可以从大数据中自动学习特征的表示，其中可以包含成千上万的参数。手工设计出有效的特征是一个相当漫长的过程。回顾计算机视觉发展的历史，往往需要五到十年才能出现一个受到广泛认可的好的特征。而深度学习可以针对新的应用从训练数据中很快学习得到新的有效的特征表示。

Embedded