Filter 过滤法

过滤型特征选择的评价标准从数据集本身的内在性质获得，与特定学习算法无关，因此具有较好的通用性。通常选择和类别相关度大的特征或特征子集进行分类或预测，降低相关度低的特征权重。

优点：算法的通用性强；省去了分类器的训练步骤，算法复杂性低，因而适用于大规模数据集；可以快速去除大量不相关的特征，作为特征的预筛选器非常合适。
缺点：忽略了特征之间可能存在的相互依赖关系。一方面，即便排序靠前的特征，如果相关性较强，则引入了冗余的特征；另一方面，排序靠后的特征，虽然独立来看作用不明显，但可能与其它特征组合起来，就有很好的预测作用，如此就损失了有价值的特征。

过滤式特征选择的评价标准分为四种：距离度量，信息度量，关联度度量，一致性度量。

方差选择法

方差选择法主要根据特征的离散程度来进行特征选择。该方法先计算个各个特征的方差，然后移除方差不满足阈值的特征。

假设我们有一个带有布尔特征的数据集，我们要移除那些超过80%的数据都为1或0的特征。布尔特征是伯努利随机变量，该类变量的方差为：

$Var[X] = p(1-p)$

sklearn默认设置下，它将移除所有方差为0的特征，即所有样本中数值完全相同的特征。而在本例中，我们将阈值设为 $.8*(1-.8)$ :

>>> from sklearn.feature_selection import VarianceThreshold
>>> X = [[0, 0, 1], [0, 1, 0], [1, 0, 0], [0, 1, 1], [0, 1, 0], [0, 1, 1]]
>>> sel = VarianceThreshold(threshold=(.8 * (1 - .8)))
>>> sel.fit_transform(X)
array([[0, 1],
       [1, 0],
       [0, 0],
       [1, 1],
       [1, 0],
       [1, 1]])

VarianceThreshold 移除了第一列特征，第一列中特征值为0的概率达到了 $p=5/6 >.8$ 。

互信息法

皮尔逊相关系数只能反映变量之间的线性相关性，互信息是变量间相互依赖性的量度，由此可以判断自变量和因变量之间的依赖程度。

自信息

自信息是与概率空间中的单一事件或离散随机变量的值相关的信息量的量度。一个随机产生的事件所包含的自信息数量，只与事件发生的概率相关。事件发生的概率越低，在事件真的发生时，接收到的信息中，包含的自信息越大。

$I(x_i)=log(\frac{1}{P(x_i)})=-log(P(x_i))$

如果事件 C中包含了两个相互独立的事件 A 与事件 B，当事件 c 发生时,它所包含的自信息量，等于事件A 的自信息量加上事件B。一系列事件的自信息加总之后，平均的自信息值就是信息熵，由此有以下定义。

熵

熵是接收的每条消息中包含的信息的平均量,是不确定性的度量，越随机的消息熵值越大。事件的概率分布和每个事件的信息量构成了一个随机变量，这个随机变量的均值（即期望）就是这个分布产生的信息量的平均值（即熵）。因此，熵可以被理解为不确定度的期望。

$H(Y)=\sum_i P(x_i)I(x_i)$

$H(Y)=-\int_YP(Y)logP(Y)=\int_YP(Y)log\frac{1}{P(Y)}$

互信息

互信息（Mutual Information，简称MI）是变量间相互依赖性的量度。当两个随机变量相互独立时，其互信息为0。不同于相关系数，互信息并不局限于实值随机变量，它更加一般且决定着联合分布 p(X,Y) 和分解的边缘分布的乘积 p(X)p(Y) 的相似程度。其定义如下：

$I(X;Y)=\int_X\int_YP(X,Y)log\frac{P(X,Y)}{P(X)P(Y)}$

互信息可以等价地表示成：

其中 $H(X)$ 和 $H(Y)$ 是边缘熵， $H(X|Y)$ 和 $H(Y|X)$ 是条件熵， $H(X,Y)$ 是X和Y的联合熵。

互信息具以下性质： 1、 $I(X;Y) >= 0$ ;

2、 $H(X)-H(X|Y)=I(X;Y)=I(Y;X)=H(Y)-H(Y|X)$

3、当$X$, $Y$独立时， $I(X;Y)=0$

4、当$X$, $Y$知道一个就能推断另一个时， $I(X;Y)=H(X)=H(Y)$

sklearn提供mutual_info_classif对互信息进行计算：

#此处利用sklearn fetch_20newsgroups的文本数据集作为例子
>>>from sklearn.datasets import fetch_20newsgroups
>>>from sklearn.feature_selection import mutual_info_classif
>>>from sklearn.feature_extraction.text import CountVectorizer
>>>categories = ['talk.religion.misc','comp.graphics', 'sci.space']
>>>newsgroups_train = fetch_20newsgroups(subset='train', categories=categories)
>>>X, Y = newsgroups_train.data, newsgroups_train.target
>>>cv = CountVectorizer(max_df=0.95, min_df=2,max_features=10000,                          stop_words='english')
>>>X_vec = cv.fit_transform(X)
>>>res = dict(zip(cv.get_feature_names(),
               mutual_info_classif(X_vec, Y, discrete_features=True)
               ))
#输出文本词汇与目标之间的互信息
>>>print(res)
>>>{'bible': 0.072327479595571439,
 'christ': 0.057293733680219089,
 'christian': 0.12862867565281702,
 'christians': 0.068511328611810071,
 'file': 0.048056478042481157,
 'god': 0.12252523919766867,
 'gov': 0.053547274485785577,
 'graphics': 0.13044709565039875,
 'jesus': 0.09245436105573257,
 'launch': 0.059882179387444862,
 'moon': 0.064977781072557236,
 'morality': 0.050235104394123153,
 'nasa': 0.11146392824624819,
 'orbit': 0.087254803670582998,
 'people': 0.068118370234354936,
 'prb': 0.049176995204404481,
 'religion': 0.067695617096125316,
 'shuttle': 0.053440976618359261,
 'space': 0.20115901737978983,
 'thanks': 0.060202010019767334}

最大信息系数法

Maximal Information Coefficient (MIC) 最大信息系数，用于衡量两个变量X和Y的线性或非线性的强度。

我们把两个随机变量化成散点图，然后不断的用小方格子去分割。然后计算每个方格子里面的落入概率。在某种意义上，就可以估计出联合概率密度分布了。当然，只有在数据量是无穷的情况下我们才可以认为是真的就相等了。所以，数据量越大，MIC越好。

最大信息系数（MIC）原理

$MIC[x;y] = max_{|X||Y|<B}\frac{I[X;Y]}{log_2(min(|X|,|Y|))}$

由上可得，MIC可度量非线性关系，取值范围是[0,1]。

MIC计算分为三个步骤：

给定i、j，对XY构成的散点图进行i列j行网格化，并求出最大的互信息值
对最大的互信息值进行归一化
选择不同尺度下互信息的最大值作为MIC值

值得注意的是，对于步骤1，给定i和j后，可以得出多种不同的网格化方案。我们需要从这些不同的网格化方案中找到使互信息最大的网格化方案。举个例子，假设i=2，j=2。则可能有以下红、黄、绿三种网格化方案（其实更多，这里只是随便挑三种方案作说明），分别计算每个网格化方案对应的互信息值，找出使互信息值最大的网格化方案。

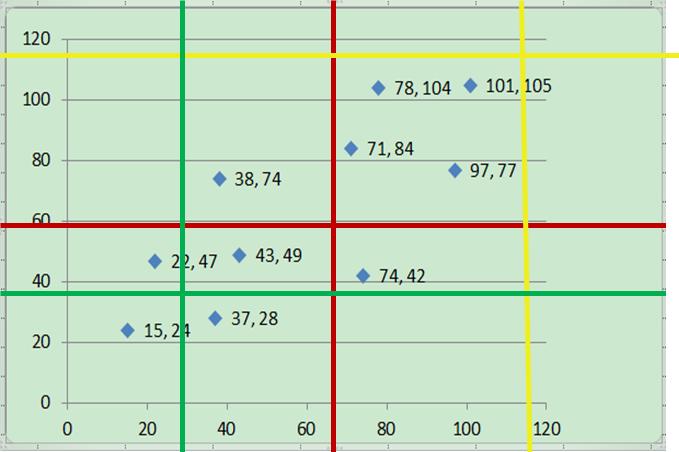
那么，给定了某个网格化方案后，如何计算其对应的互信息值呢？这里以上图中红色的网格化方案为例进行说明。红色网格化方案将所有数据点分为四个区域：左上，右上，左下，右下。每个区域对应的数据点数量为1，4，4，1。将数据点数归一化得到四个区域的数据点频率，分别为0.1，0.4，0.4，0.1。也就是说，此时，X有两种取值：左和右，Y有两种取值：上和下。P(X=左,Y=上)=0.1，P(X=右,Y=上)=0.4，P(X=左,Y=下)=0.4，P(X=右,Y=下)=0.1。并且，P(X=左)=0.5，P(X=右)=0.5，P(Y=上)=0.5，P(Y=下)=0.5。根据前面介绍的互信息计算公式，得到X和Y在这种分区下的互信息为：

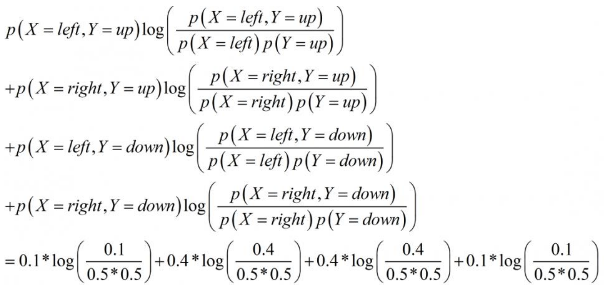
以此类推，算出哪种方案得到的互信息值最大，最大的互信息值是多少。D表示数据点集。

再回来看刚才定义的公式：

$MIC[x;y] = max_{|X||Y|<B}\frac{I[X;Y]}{log_2(min(|X|,|Y|))}$

|X|表示X方向共被分割成几段，|Y|同理。

|X|*|Y|< B 表示所有的方格数目要小于B。

B是一个经验值，一般取数据总量的0.6或者0.55次方。

MIC总结

MIC具有普适性、公平性和对称性。

所谓普适性，是指在样本量足够大(包含了样本的大部分信息)时，能够捕获各种各样的有趣的关联，而不限定于特定的函数类型(如线性函数、指数函数或周期函数)，或者说能均衡覆盖所有的函数关系。一般变量之间的复杂关系不仅仅是通过单独一个函数就能够建模的，而是需要叠加函数来表现。

所谓公平性，是指在样本量足够大时能为不同类型单噪声程度相似的相关关系给出相近的系数。例如，对于一个充满相同噪声的线性关系和一个正弦关系，一个好的评价算法应该给出相同或相近的相关系数。
下面是MIC与Pearson系数的比较。

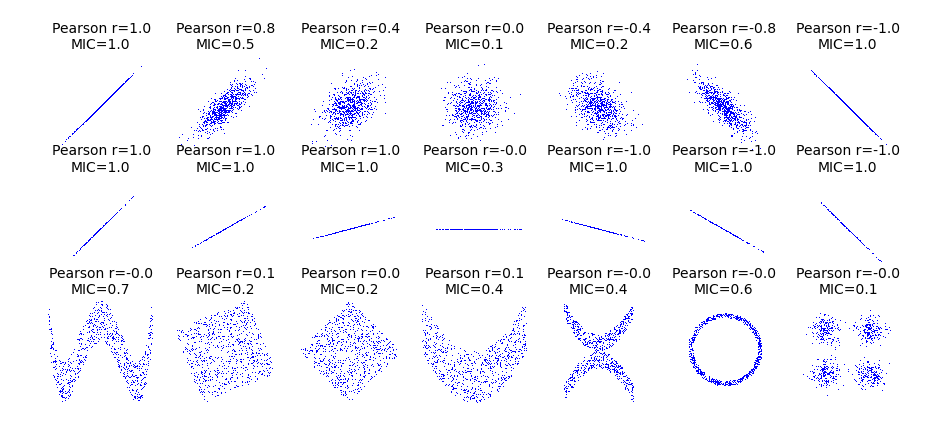
从上图可以看出，MIC对变量间关系的判断表现明显优于Pearson系数。

使用feature_selection库的SelectKBest类结合最大信息系数法来选择特征的代码如下：

from sklearn.feature_selection import SelectKBest
from minepy import MINE

#由于MINE的设计不是函数式的，定义mic方法为函数式的，返回一个二元组，二元组的第2项设置成固定的P值0.5
 def mic(x, y):
     m = MINE()
     m.compute_score(x, y)
     return (m.mic(), 0.5)

#选择K个最好的特征，返回特征选择后的数据
SelectKBest(lambda X, Y: array(map(lambda x:mic(x, Y), X.T)).T, k=2).fit_transform(iris.data, iris.target)

卡方检验法

经典的卡方检验是检验定性自变量对定性因变量的相关性。假设自变量有N种取值，因变量有M种取值，考虑自变量等于i且因变量等于j的样本频数的观察值与期望的差距，构建统计量： $\chi^2=\sum\frac{(A-E)^2}{E}$

上式中A表示观察值，E表示期望。不难发现，这个统计量的含义就是自变量对因变量的相关性。用feature_selection库的SelectKBest类结合卡方检验来选择特征的代码如下：

from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import chi2

#选择K个最好的特征，返回选择特征后的数据
SelectKBest(chi2, k=2).fit_transform(iris.data, iris.target)

Fisher Score

对特征进行fisher得分的计算并排序，选择得分最高的前若干个特征。

#pip install skfeature-chappers
>>> from skfeature.function.similarity_based import fisher_score
>>> from sklearn.datasets import load_iris
>>> iris = load_iris()
>>> X, y = iris.data, iris.target
>>> score = fisher_score.fisher_score(X, y)
>>>print(score)
[1 0 3 2]

FastRegression

FastRegression主要被应用于因变量为连续值的情况，它利用线性模型测试单个特征对目标值的回归效果，然后对不同的特征进行排序。

自变量i与因变量的样本相关系数 $r_i$ 为：

$r_i=\frac{(X_i-\overline{X_i})^T(y-\overline{y})}{\sigma_{Xi}\sigma_y}$

式中 $X_i$ 表示所有样本在第i个特征上的取值的向量， $y$ 为所有样本对应的标签的向量， $\sigma_{X_i}、\sigma_y$ 分别为 $X_i$ 和 $y$ 的标准差。

那么，回归效果对应的 $f$ 值为：

$f=\frac{r_i^2}{1-r_i^2}*(n-2)$

用feature_selection库的SelectKBest类结合FastRegression来实现特征选择的代码如下：

>>> from sklearn.feature_selection import SelectKBest, f_regression
>>> from sklearn.datasets import load_iris
>>> iris = load_iris()
>>> X, y = iris.data, iris.target
>>> X.shape
(150, 4)
#利用回归选择排序前三的的特征
>>> feat_selector = SelectKBest(f_regression, k=3)
>>> feat_selector.fit(X,y)
SelectKBest(k=3, score_func=<function f_regression at 0x000001DA46CB5EA0>)
#查看回归拟合每个数据的f值
>>> feat_selector.scores_
array([  233.8389959 ,    31.59750825,  1342.15918918,  1589.55920433])
#查看回归拟合每个数据的p值
>>> feat_selector.pvalues_
array([  2.89047835e-32,   9.15998497e-08,   4.15547758e-76,
         4.77500237e-81])
#查看特征选择的结果
>>> feat_selector.get_support()
array([ True, False,  True,  True], dtype=bool)

Filter

Filter 过滤法

方差选择法

相关系数法

互信息法

最大信息系数法

卡方检验法

Fisher Score

FastRegression

参考资料

results matching ""

No results matching ""