特征Hash

在特征处理中，通常会利用笛卡尔乘积的方法来构造组合特征，这种方法虽然简单，但会使得特征数量爆炸式增长。比如一个可以取N个不同值的类别特征，与一个可以去M个不同值的类别特征做笛卡尔乘积，就能构造出N*M个组合特征。

特征太多这个问题在具有个性化的问题里尤为突出。如果把用户id看成一个类别特征，那么它可以取的值的数量就等于用户数。把这个用户id特征与其他特征做笛卡尔积，就能产生庞大的特征集。

对于特征数量过多的问题，目前已经有很多用于降维的方法，比如聚类、PCA等都是常用的降维方法。但这类方法在特征量和样本量很多的时候本身就计算量很大，所以对大问题也基本无能为力。

因此，本文介绍一种很简单的降维方法——特征哈希（Feature Hashing）法。

特征哈希法的目标是把原始的高维特征向量压缩成较低维特征向量，且尽量不损失元素特征值的表达能力。

原理

记哈希前的特征向量为$x \in \sf{R}^N$。我们要把这个原始的N维特征向量压缩成M维（M < N）。 记$h(n): \{1, …, N\} \rightarrow \{1, …, M\}$ 为一个选定的均匀哈希函数，而$\xi(n): \{1, …, N\} \rightarrow \{-1, 1\}$为另一个选定的均匀哈希函数。$h(n)$和$\xi(n)$是独立选取的，它们之间没关系。按下面方式计算哈希后的M维新特征向量$\phi \in \sf{R}^M$的第$i$个元素值（$\phi$是依赖于$x$的，所以有时候也把$\phi$写成$\phi(x)$）：

​ $\phi_i = \sum_{j:\ h(j)=i} \xi(j) \ x_j$

​ $x^Tx' \approx \phi^T\phi'$

​ $||x-x'|| \approx ||\phi-\phi'||$

其中$x$和$x’$为两个原始特征向量，而$\phi$和$\phi’$为对应的哈希后的特征向量。

利用上面的哈希方法把$x$转变成$\phi$后，就可以直接把$\phi$用于机器学习算法了。这就是利用特征哈希法来降低特征数量的整个过程。需要说的是，这里面的两个哈希函数$h$和$\xi$并不要求非要是把整数哈希成整数，其实它们只要能把原始特征均匀哈希到新特征向量上就行。例如在NLP里，每个特征代表一个单词，那么只要保证$h$和$\xi$把单词均匀哈希到$\{1, …, M\}$和$\{-1, 1\}$就行。

Python实现

当特征取值列表很大，且有多个需onehot编码时，会导致特征矩阵很大，且有很多0，这时可用哈希函数将特征根据特征名和值映射到指定维数的矩阵。由于hash是单向函数，因此FeatureHash没有inverse_transform函数。

from sklearn.feature_extraction import FeatureHasher
h = FeatureHasher(n_features=10,input_type='dict')
D = [{'dog': 1, 'cat':2, 'elephant':4},{'dog': 2, 'run': 5}]
f = h.transform(D)
f.toarray()
>>>array([[ 0.,  0., -4., -1.,  0.,  0.,  0.,  0.,  0.,  2.],
          [ 0.,  0.,  0., -2., -5.,  0.,  0.,  0.,  0.,  0.]])

n_features：输出矩阵的特征数（列数）。

input_type：指定输入数据的类型，dict、pair或者string，默认值为‘dict’。

transform()：把输入数据转换为稀疏矩阵。

实际应用

下面具体说明如何把特征哈希法应用于多任务学习（multitask learning）问题。所谓多任务学习，就是同时求解多个问题。个性化问题就是一种典型的多任务学习问题，它同时学习多个用户的兴趣偏好。

在世纪佳缘我们使用Logistic Regression (LR) 模型学习每个男性用户的交友兴趣以便预测他给具有某些特征的女性的发信概率。这时候学习一个男性用户的交友兴趣就是一个学习任务。记男性用户集合为$\bf U$，抽取出的女性特征维度为$d$。我们为每个用户$u \in \bf U$学习一组参数$w_u \in \sf{R}^d$。再加上一组全局参数$w_0$，总共有$N \triangleq d \cdot (1+\mid \bf{U} \mid)$个参数。这种表达方式就是把男性用户id与所有特征$x$做了笛卡尔积。下图给出了一个有3个用户且$x$长度为2时扩展后各个用户对应特征向量的示例图。LR模型通过计算$(w_0 + w_u)^T x$来获得最终的预测概率值。

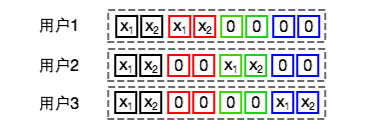
这个问题也可以转化到特征哈希后的空间来看。我们为每个用户引入一个不同的转换函数$\phi_u(x)$。一般取$\phi_u(x)=\phi((u, x))$即可。那么用户$u$对应的扩展向量通过哈希转换后为

​ $x^h_u \triangleq \phi_0(x) + \phi_u(x)$

扩展向量对应的权重参数$[w_0^T, \ldots, w_{\mid \bf{U} \mid}^T]$通过哈希转换后为

​ $w^h \triangleq \phi_0(w_0) + \sum_{u \in \bf{U}} \phi_u(w_u)$

那么在哈希转换后的空间里，

​ $(w^h)^Tx_u^h = \left(\phi_0(w_0) + \sum_{u \in \bf{U}} \phi_u(w_u)\right)^T \left(\phi_0(x)+\phi_u(x)\right) \\ \approx \phi_0(w_0)^T \phi_0(x) + \phi_u(w_u)^T \phi_u(x) \\ \approx w_0^Tx + w_u^Tx \\ =(w_0+w_u)^Tx$

​ $\phi_u(w_u)^T \phi_{u'}(x) \approx 0 , \ \forall u \neq u'$

具体实现算法时，我们并不需要关心$w^h$，只需要把原始特征$x$通过哈希转换成$x^h_u$即可，剩下的就是标准机器学习流程了。

总结

特征哈希法的优点有：

• 可以降低特征数量，从而加速算法训练与预测过程，以及降低内存消耗；
• 相比较与one-hot encoding，不需要预先维护一个变量表；
• 在线学习方便，实现简单，所需额外计算量小；
• 可以添加新的任务（如新用户），或者新的原始特征而保持哈希转换后的特征长度不变，很适合任务数频繁变化的问题（如个性化推荐里新用户，新item的出现）；
• 可以保持原始特征的稀疏性，哈希转换时只有非0原始特征才起作用；
• 可以只哈希转换其中的一部分原始特征，而保留另一部分原始特征（如那些出现collision就会很影响精度的重要特征）。

与此同时，特征哈希也存在一些不足：

• 通过哈希转换后学习的模型变得很难检验，我们很难对训练出的模型参数做出合理解释；
• 它会把多个原始特征哈希到相同的位置上，出现哈希里的collision现象，不过实际实验表明这种collision对算法的精度影响很小。特征哈希将高维稀疏的解空间压缩到低维稠密的空间，压缩到的维度越低，越容易发生碰撞，此时可通过使用多个哈希函数维护多张哈希表来减少碰撞造成的信息损失。

参考资料

1. 特征哈希(Feature Hashing)
2. Trevor Hastie et al. The Elements of Statistical Learning, 2001.
3. Kilian Weinberger et al. Feature Hashing for Large Scale Multitask Learning, 2010.
4. Joshua Attenberg et al. Collaborative Email-Spam Filtering with the Hashing-Trick, 2009.
5. https://www.zhihu.com/question/264165760/answer/277634591
6. sklearn.feature_extraction.FeatureHasher
7. sklearn学习笔记2 Feature_extraction库
8. 特征选择和稀疏学习
9. 《西瓜书》笔记11：特征选择与稀疏表示（三）
10. 特征选择与稀疏学习
11. https://www.zhihu.com/question/24124122/answer/50403932
12. https://blog.csdn.net/u014595019/article/details/52433754
13. PCA算法详解
14. 主成分分析（PCA）原理详解
15. 主成分分析PCA算法：为什么去均值以后的高维矩阵乘以其协方差矩阵的特征向量矩阵就是“投影”？
16. 用Python的sklearn库进行PCA(主成分分析)
17. 用scikit-learn学习主成分分析(PCA)
18. 独立成分分析（Independent Component Analysis）
19. 独立成分分析 ( ICA ) 与主成分分析 ( PCA ) 的区别在哪里？
20. 独立成分分析ICA系列4:ICA的最优估计方法综述
21. ICA-独立成分分析
22. 独立成分分析Independent component analysis(ICA)
23. 线性判别分析LDA原理总结
24. 一文读懂特征工程
25. 线性判别分析LDA详解
26. LinearDiscriminantAnalysis
27. 用scikit-learn进行LDA降维
28. https://blog.csdn.net/u010705209/article/details/53518772
29. https://blog.csdn.net/u012162613/article/details/42214205
30. https://blog.csdn.net/qianhen123/article/details/40077873
31. https://github.com/ceys/jdml/wiki/ALS
32. 美团点评技术团队之深入FFM原理与实践
33. [深度学习笔记（一）稀疏自编码器] (https://blog.csdn.net/u010278305/article/details/46881443)
34. Field-aware Factorization Machines for CTR Prediction ,Yuchin Juan et al.
35. Factorization Machines, Steffen Rendle et al.[2010]
36. http://deeplearning.stanford.edu/wiki/index.php/UFLDL_Tutorial
37. 局部线性嵌入(LLE)原理总结
38. Locally linear embedding(LLE)局部线性嵌入-降维
39. LocallyLinearEmbedding
40. 用scikit-learn研究局部线性嵌入(LLE)
41. 聚类和降维的区别与联系
42. 聚类算法
43. 受限玻尔兹曼机（RBM）学习笔记
44. 受限制玻尔兹曼机RBM原理简介
45. 从SNE到t-SNE
46. t-SNE完整笔记
47. SNE降维与可视化
48. 比PCA降维更高级 —— t-SNE聚类算法实现指南