非线性特征降维——LLE

LLE局部线性嵌入

局部线性嵌入(Locally Linear Embedding, 简称为LLE)是非常重要的降维方法。和传统的PCA，LDA等关注样本方差的降维方法相比，LLE关注于降维时保持样本局部的线性特征，由于LLE在降维时保持了样本的局部特征，它广泛的用于图像图像识别，高维数据可视化等领域。下面，我先对LLE进行算法描述，然后从算法原理和代码实现两个方面对LLE进行总结。

LLE算法描述

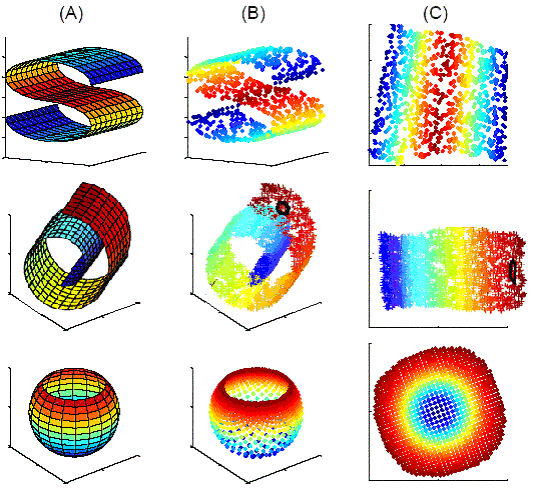
LLE 算法可以由下图所示的一个例子来描述。在下图中，LLE成功地将三维非线性数据映射到二维空间中（图B映射到图C）。如果把B中红颜色和蓝颜色的数据分别看成是分布在三维空间中的两类数据，则在通过LLE算法降维后，数据在二维空间中仍能保持相对独立的两类。观察第二行的几幅图，如果将B的黑色小圈中的数据映射到二维空间中，则为C中的黑色小圈中的数据。映射后的数据仍然能保持原有的数据流形，这说明LLE算法能够保持流形的领域不变性。LLE算法操作简单，且算法中的优化不涉及到局部最小化。该算法能解决非线性映射，但是，当处理数据的维数过大，数量过多，涉及到的稀疏矩阵过大，也不易于处理。观察第三行的几幅图，在图B的球形面中，当缺少北极面时，应用LLE算法则能很好的将其映射到二维空间中（如图C）。但如果数据分布在整个封闭的球面上，LLE则不能在保持原有的数据流形的情况下，将它们映射到二维空间中。所以我们在用LLE处理数据时，首先要假设数据不是分布在闭合的球面或者椭球面上。

image

LLE算法原理

LLE思想

首先我们先来看看LLE的算法思想。

LLE首先假设数据在较小的局部是线性的，也就是说，某一个数据可以由它领域中的几个样本来线性表示。比如我们有一个样本，我们在它的原始高维邻域里用K-近邻思想找到和它最近的三个样本。然后我们假设可以由线性表示，即：

其中为权重系数。在我们通过LLE降维之后，我们希望在低维空间对应的投影 和对应的投影也尽量保持相同的线性关系，即:

也就是说，投影前后线性关系的权重系数是尽量不变或者最小改变的。

从上面可以看出，线性关系只在样本的附近起作用，离样本远的样本对局部的线性关系没有影响，因此降维的复杂度降低了很多。

下面我们推导LLE算法的过程。

LLE算法推导

对于LLE算法，我们首先要确定邻域大小的选择，即我们需要多少个邻域样本来线性表示某个样本。假设这个值为k。我们可以通过和KNN一样的思想通过距离度量比如欧式距离来选择某样本的k个最近邻。 在寻找到某个样本的的k个最近邻之后我们就需要找到和这k个最近邻之间的线性关系，也就是要找到线性关系的权重系数。找线性关系，这显然是一个回归问题。假设我们有m个n维样本，我们可以用均方差为回归问题的损失函数，即：

一般我们也会对权重系数做归一化的限制，即权重系数需要满足

对于不在样本邻域内的样本，我们令对应的。

也就是我们需要通过上面两个式子求出我们的权重系数。一般我们可以通过矩阵和拉格朗日乘子法来求解这个最优化问题。

对于第一个式子，我们先将其矩阵化:

其中。

我们令矩阵，则第一个式子进一步化简为：

对于第二个式子，我们可以矩阵化为：

其中为k维全1向量。

现在我们将矩阵化的两个式子用拉格朗日乘子法合为一个优化目标：

对求导并令其值为0，我们得到

即我们的

其中为一个常数。利用，对归一化，那么最终我们的权重系数为

现在我们得到了高维度的权重系数，那么我们希望这些权重系数对应的线性关系在降维后一样得到保持。假设我们的n维样本集，在低维度对应的投影为，则我们希望保持线性关系，也就是希望对应的均方差损失函数最小，即最小化损失函数，如下：

可以看到这个式子和我们在高维的损失函数几乎相同，唯一的区别是高维的式子中，高维数据已知，目标是求最小值对应的权重系数，而我们在低维是权重系数已知，要求出对应的低维数据。 为了得到标准化的低维数据，一般我们也会加入如下的约束条件：

首先我们将目标函数矩阵化：

如果我们令，则优化函数转变为最小化下式：

其中tr为迹函数。约束函数矩阵化为：。

如果大家熟悉PCA的优化，就会发现这里的优化过程几乎一样。其实最小化J(Y)对应的Y就是M的最小的d个特征值所对应的d个特征向量组成的矩阵。当然我们也可以用拉格朗日乘子法得到这个式子：

对Y求导并令其为0，我们得到，即，这样我们就很清楚了，要得到最小的d维数据集，我们需要求出矩阵M最小的d个特征值所对应的d个特征向量组成的矩阵，即可。 一般的，由于M的最小特征值为0不能反映数据特征，此时特征向量全为1。我们通常选择M的第二个到第d+1个最小的特征值对应的特征向量来得到最终的。为什么M的最小特征值为0呢？这是因为，得到。由于，所以只有，即，两边同时右乘，即可得到，即M的最小特征值为0。

LLE算法流程

在上一节我们已经基本推导了LLE降维的整个过程，现在我们对算法过程做一个总结。整个LLE算法用一张图可以表示如下：

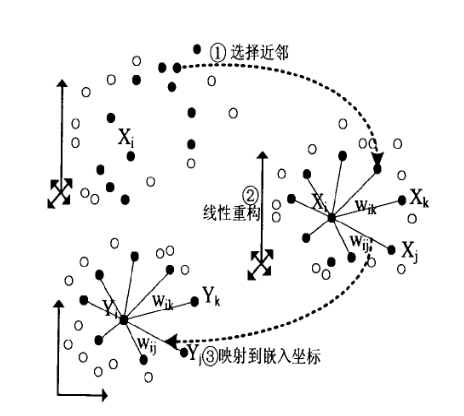
image

从图中可以看出，LLE算法主要分为3步，第一步是求K近邻的过程，这个过程使用了和KNN算法一样的求最近邻的方法。第二步，就是对每个样本求它在邻域里的K个近邻的线性关系，得到线性关系权重系数W。第三步就是利用权重系数来在低维里重构样本数据。 具体过程如下：

输入：样本集，最近邻数k，降维到的维数d

输出：低维样本集矩阵

  1. 枚举每一个样本，按欧式距离作为度量，计算和最近的k个最近邻

  2. 枚举每一个样本，求出局部协方差矩阵，并求出对应的权重系数向量：

  3. 由权重系数向量组成权重系数矩阵，计算矩阵

  4. 计算矩阵M的前d+1个特征值，并计算这d+1个特征值对应的特征向量

  5. 由第二个特征向量到第d+1个特征向量张成的矩阵即为输出低维样本集矩阵

LLE的python实现

在scikit-learn中，sklearn.manifold包中有流形学习库。而该库就实现了LLE算法。

LLE算法类LocallyLinearEmbedding使用起来并不复杂，一般来说，需要调参的参数只有样本近邻的个数。下面我们对LocallyLinearEmbedding的主要参数做一个介绍。

  1. n_neighbors: 即我们搜索样本的近邻的个数，默认是5。 n_neighbors个数越大，则建立样本局部关系的时间会越大，也就意味着算法的复杂度会增加。当然n_neighbors个数越大，则降维后样本的局部关系会保持的更好。在下一节我们可以通过具体的例子看出这一点。一般来说，如果算法运行时间可以接受，我们可以尽量选择一个比较大一些的n_neighbors。
  2. n_components: 即我们降维到的维数。如果我们降维的目的是可视化，则一般可以选择2-5维。
  3. reg: 正则化系数，在n_neighbors大于n_components时，即近邻数大于降维的维数时，由于我们的样本权重矩阵不是满秩的，LLE通过正则化来解决这个问题。默认是0.001。一般不用管这个参数。当近邻数远远的大于降维到的维数时可以考虑适当增大这个参数。
  4. eigen_solver: 特征分解的方法。有‘arpack’和‘dense’两者算法选择。当然也可以选择‘auto‘让scikit-learn自己选择一个合适的算法。‘arpack’和‘dense’的主要区别是‘dense’一般适合于非稀疏的矩阵分解。而‘arpack’虽然可以适应稀疏和非稀疏的矩阵分解，但在稀疏矩阵分解时会有更好算法速度。当然由于它使用一些随机思想，所以它的解可能不稳定，一般需要多选几组随机种子来尝试。
  5. method: 即LLE的具体算法。LocallyLinearEmbedding支持4种不同的LLE算法。
  6. neighbors_algorithm: 这个是k近邻的搜索方法，和KNN算法的使用的搜索方法一样。

下面我们用一个具体的例子来使用scikit-learn进行LLE降维并可视化。

首先载入需要的库;

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
%matplotlib inline
from sklearn import manifold, datasets
from sklearn.utils import check_random_state

接着生成随机数据，由于LLE必须要基于流形不能闭合，因此我们生成了一个缺一个口的三维球体。生成数据并可视化的代码如下：

n_samples = 500
random_state = check_random_state(0)
p = random_state.rand(n_samples) * (2 * np.pi - 0.55)
t = random_state.rand(n_samples) * np.pi

# 让球体不闭合，符合流形定义
indices = ((t < (np.pi - (np.pi / 8))) & (t > ((np.pi / 8))))
colors = p[indices]
x, y, z = np.sin(t[indices]) * np.cos(p[indices]),     np.sin(t[indices]) * np.sin(p[indices]),     np.cos(t[indices])

fig = plt.figure()
ax = Axes3D(fig, elev=30, azim=-20)
ax.scatter(x, y, z, c=p[indices], marker='o', cmap=plt.cm.rainbow)

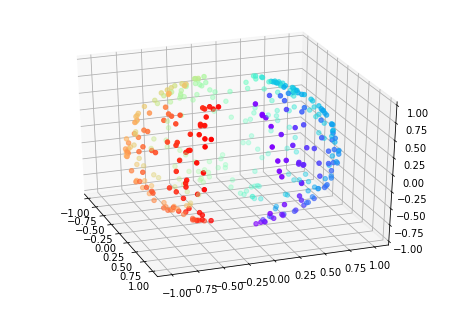
image

上图是原始数据的分布图。

现在我们简单的尝试用LLE将其从三维降为2维并可视化，近邻数设为30，用标准的LLE算法。

train_data = np.array([x, y, z]).T
trans_data = manifold.LocallyLinearEmbedding(n_neighbors =30, n_components = 2,
                                method='standard').fit_transform(train_data)
plt.scatter(trans_data[:, 0], trans_data[:, 1], marker='o', c=colors)

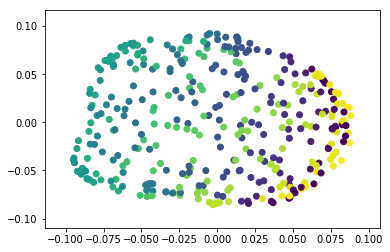
image

上图为降维到2维后的效果图。

可以看出从三维降到二维后，我们大概还是可以看出这是一个球体。

LLE总结

LLE是广泛使用的图形图像降维方法，它实现简单，但是对数据的流形分布特征有严格的要求。比如不能是闭合流形，不能是稀疏的数据集，不能是分布不均匀的数据集等等，这限制了它的应用。下面总结下LLE算法的优缺点。

LLE算法的主要优点有：

  1. 可以学习任意维的局部线性的低维流形。
  2. 算法归结为稀疏矩阵特征分解，计算复杂度相对较小，实现容易。

LLE算法的主要缺点有：

  1. 算法所学习的流形只能是不闭合的，且样本集是稠密均匀的。
  2. 算法对最近邻样本数的选择敏感，不同的最近邻数对最后的降维结果有很大影响。

参考资料

  1. 特征哈希(Feature Hashing)
  2. Trevor Hastie et al. The Elements of Statistical Learning, 2001.
  3. Kilian Weinberger et al. Feature Hashing for Large Scale Multitask Learning, 2010.
  4. Joshua Attenberg et al. Collaborative Email-Spam Filtering with the Hashing-Trick, 2009.
  5. https://www.zhihu.com/question/264165760/answer/277634591
  6. sklearn.feature_extraction.FeatureHasher
  7. sklearn学习笔记2 Feature_extraction库
  8. 特征选择和稀疏学习
  9. 《西瓜书》笔记11：特征选择与稀疏表示（三）
  10. 特征选择与稀疏学习
  11. https://www.zhihu.com/question/24124122/answer/50403932
  12. https://blog.csdn.net/u014595019/article/details/52433754
  13. PCA算法详解
  14. 主成分分析（PCA）原理详解
  15. 主成分分析PCA算法：为什么去均值以后的高维矩阵乘以其协方差矩阵的特征向量矩阵就是“投影”？
  16. 用Python的sklearn库进行PCA(主成分分析)
  17. 用scikit-learn学习主成分分析(PCA)
  18. 独立成分分析（Independent Component Analysis）
  19. 独立成分分析 ( ICA ) 与主成分分析 ( PCA ) 的区别在哪里？
  20. 独立成分分析ICA系列4:ICA的最优估计方法综述
  21. ICA-独立成分分析
  22. 独立成分分析Independent component analysis(ICA)
  23. 线性判别分析LDA原理总结
  24. 一文读懂特征工程
  25. 线性判别分析LDA详解
  26. LinearDiscriminantAnalysis
  27. 用scikit-learn进行LDA降维
  28. https://blog.csdn.net/u010705209/article/details/53518772
  29. https://blog.csdn.net/u012162613/article/details/42214205
  30. https://blog.csdn.net/qianhen123/article/details/40077873
  31. https://github.com/ceys/jdml/wiki/ALS
  32. 美团点评技术团队之深入FFM原理与实践
  33. [深度学习笔记（一）稀疏自编码器] (https://blog.csdn.net/u010278305/article/details/46881443)
  34. Field-aware Factorization Machines for CTR Prediction ,Yuchin Juan et al.
  35. Factorization Machines, Steffen Rendle et al.[2010]
  36. http://deeplearning.stanford.edu/wiki/index.php/UFLDL_Tutorial
  37. 局部线性嵌入(LLE)原理总结
  38. Locally linear embedding(LLE)局部线性嵌入-降维
  39. LocallyLinearEmbedding
  40. 用scikit-learn研究局部线性嵌入(LLE)
  41. 聚类和降维的区别与联系
  42. 聚类算法
  43. 受限玻尔兹曼机（RBM）学习笔记
  44. 受限制玻尔兹曼机RBM原理简介
  45. 从SNE到t-SNE
  46. t-SNE完整笔记
  47. SNE降维与可视化
  48. 比PCA降维更高级 —— t-SNE聚类算法实现指南

results matching ""

    No results matching ""