线性特征降维——FM

FM/FFM

FM(因子分解机)

FM基本原理

因子分解机最早在2010年由德国康斯坦茨大学的Steffen Rendle提出，应用于大规模稀疏数据的特征组合问题。在分析FM算法的原理和实现细节之前，我们先来了解稀疏数据是如何产生的。

举一个简单的例子，我们在前面的数据整理中有提到过，训练机器学习模型之前要把一些定性数据转化为定量特征，通过one-hot编码后，一个一维的类别特征可以变换为数十维的数值特征，其中大部分的元素都是零，即稀疏的。另一方面稀疏的数据也会占用大量的内存资源。

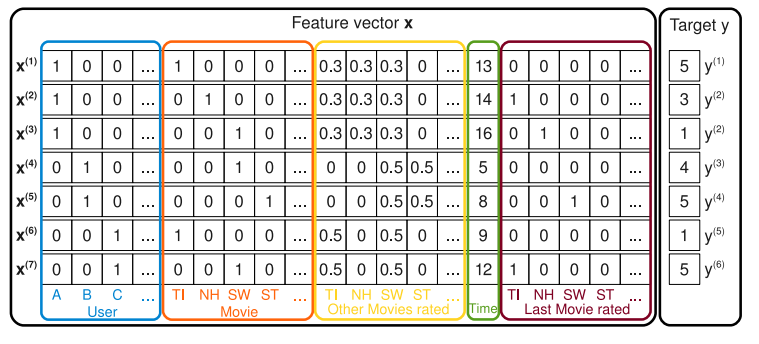
假设一个广告分类的问题，根据用户和广告位相关的特征，预测用户是否点击了广告。某些特征经过关联后，与label直接的相关性就会提高，例如，“USA”与“Thanksgiving”、“China”与“Chinese New Year”。这种关联性在实际问题是普遍存在的，“化妆品”与“女性”，“运动”与“男性”。因此，非常有必要引入两个特征的组合。

在这里，我们讨论度为2的多项式模型，其定义为： $\hat{y}(x) = w_0+\sum_{i=1}^{n}w_ix_i + \sum_{i=1}^{n}\sum_{j=i+1}^{n}w_{ij}x_ix_j$

其中n代表样本的特征数量，$x_i$是第$i$个特征的值，$w_0$、$w_i$、$w_{ij}$，是模型参数。不难看出，组合特征的参数一共有$\frac{n(n-1)}{2}$个，每个参数的训练都需要大量非零的样本，但样本数据本来就非常稀疏，样本不足会导致参数不准确，严重影响模型性能。

为了解决二次项参数训练的问题，我们引入一种矩阵分解的办法：当$W$为对称正定矩阵时，存在矩阵$V$，使得$W=V^TV$。所以FM模型可以表示为： $\hat{y}(x) = w_0+\sum_{i=1}^{n}w_ix_i + \sum_{i=1}^{n}\sum_{j=i+1}^{n}\langle v_i,v_j \rangle x_ix_j$

其中，$v_i$是第$i$维特征的隐向量，$\langle ,\rangle$代表向量点积，隐向量的长度为$k(k<<n)$。组合特征的二次项还可以进行如下的化简：

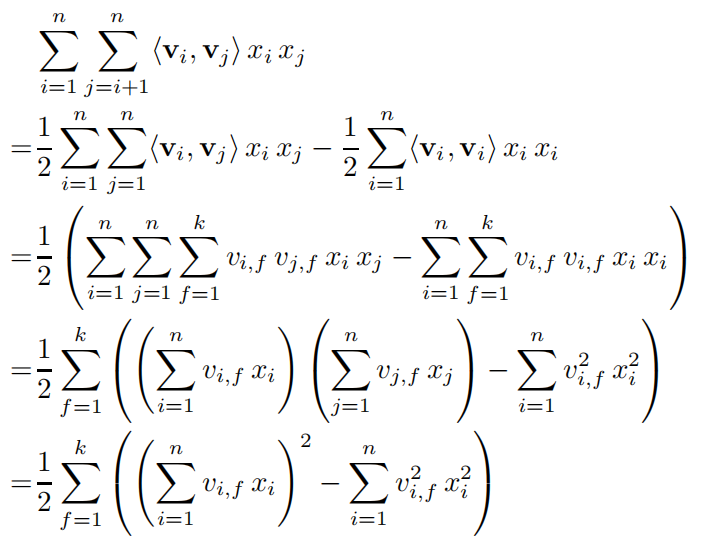
在化简后，模型的复杂度降为$O(kn)$，说明FM模型可以在线性时间内完成对样本的预测。利用$SGD$训练模型： $\frac{\partial}{\partial\theta}\hat{y}(x)= \begin{cases} 1& \text{if $\theta$ is $w_0$}\\ x_i& \text{if $\theta$ is $w_i$}\\ x_i\sum_{j=1}^{n}v_{j,f}x_j-v_{i,f}x_i^2 & \text{if $\theta$ is $v_{i,f}$} \end{cases}$

FFM

FFM基本原理(交叉组合特征)

FFM是FM的升级版，通过引入场域的概念，把相同性质的特征归于同一个field，简单的来说，被one-hot编码的特征都可以归于同一个field。每一维特征$x_i$，针对不同的field，都会学习一个隐向量$v_{i,f_j}$，其模型定义为： $\hat{y}(x) = w_0+\sum_{i=1}^{n}w_ix_i + \sum_{i=1}^{n}\sum_{j=i+1}^{n}\langle v_{i,f_j},v_{j,f_i} \rangle x_ix_j$ $f_j$ 是第 $j$ 个特征所属的field。如果隐向量的长度为$k$，那么FFM的二次参数有$nfk$ 个，远多于FM模型的 $nk$ 个。此外，由于隐向量与field相关，FFM二次项并不能够化简，其预测复杂度是$O(kn^2)$。

SGD训练FFM的算法为：

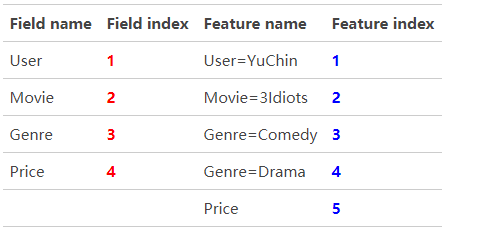
举一个简单例子说明FFM的特征组合方式，一条输入记录如下：

这条记录可以编码成5个特征：

FFM的组合特征有10项：

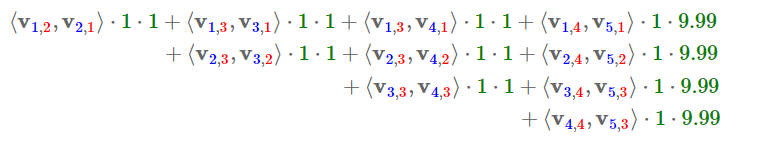
参考资料

1. 特征哈希(Feature Hashing)
2. Trevor Hastie et al. The Elements of Statistical Learning, 2001.
3. Kilian Weinberger et al. Feature Hashing for Large Scale Multitask Learning, 2010.
4. Joshua Attenberg et al. Collaborative Email-Spam Filtering with the Hashing-Trick, 2009.
5. https://www.zhihu.com/question/264165760/answer/277634591
6. sklearn.feature_extraction.FeatureHasher
7. sklearn学习笔记2 Feature_extraction库
8. 特征选择和稀疏学习
9. 《西瓜书》笔记11：特征选择与稀疏表示（三）
10. 特征选择与稀疏学习
11. https://www.zhihu.com/question/24124122/answer/50403932
12. https://blog.csdn.net/u014595019/article/details/52433754
13. PCA算法详解
14. 主成分分析（PCA）原理详解
15. 主成分分析PCA算法：为什么去均值以后的高维矩阵乘以其协方差矩阵的特征向量矩阵就是“投影”？
16. 用Python的sklearn库进行PCA(主成分分析)
17. 用scikit-learn学习主成分分析(PCA)
18. 独立成分分析（Independent Component Analysis）
19. 独立成分分析 ( ICA ) 与主成分分析 ( PCA ) 的区别在哪里？
20. 独立成分分析ICA系列4:ICA的最优估计方法综述
21. ICA-独立成分分析
22. 独立成分分析Independent component analysis(ICA)
23. 线性判别分析LDA原理总结
24. 一文读懂特征工程
25. 线性判别分析LDA详解
26. LinearDiscriminantAnalysis
27. 用scikit-learn进行LDA降维
28. https://blog.csdn.net/u010705209/article/details/53518772
29. https://blog.csdn.net/u012162613/article/details/42214205
30. https://blog.csdn.net/qianhen123/article/details/40077873
31. https://github.com/ceys/jdml/wiki/ALS
32. 美团点评技术团队之深入FFM原理与实践
33. [深度学习笔记（一）稀疏自编码器] (https://blog.csdn.net/u010278305/article/details/46881443)
34. Field-aware Factorization Machines for CTR Prediction ,Yuchin Juan et al.
35. Factorization Machines, Steffen Rendle et al.[2010]
36. http://deeplearning.stanford.edu/wiki/index.php/UFLDL_Tutorial
37. 局部线性嵌入(LLE)原理总结
38. Locally linear embedding(LLE)局部线性嵌入-降维
39. LocallyLinearEmbedding
40. 用scikit-learn研究局部线性嵌入(LLE)
41. 聚类和降维的区别与联系
42. 聚类算法
43. 受限玻尔兹曼机（RBM）学习笔记
44. 受限制玻尔兹曼机RBM原理简介
45. 从SNE到t-SNE
46. t-SNE完整笔记
47. SNE降维与可视化
48. 比PCA降维更高级 —— t-SNE聚类算法实现指南