线性特征降维——ICA
ICA独立成分分析
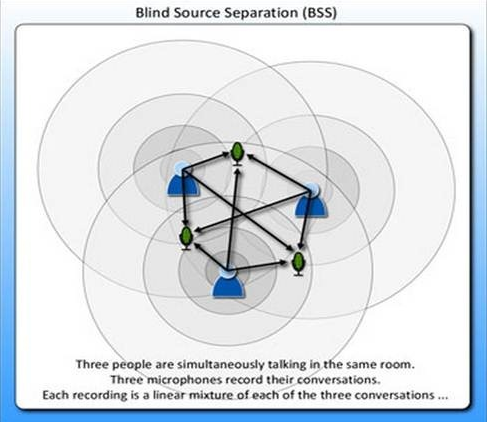
独立成分分析(Independent Component Analysis),最早应用于盲源信号分离(Blind Source Separation,BBS)。起源于“鸡尾酒会问题”,描述如下:在嘈杂的鸡尾酒会上,许多人在同时交谈,可能还有背景音乐,但人耳却能准确而清晰的听到对方的话语。这种可以从混合声音中选择自己感兴趣的声音而忽略其他声音的现象称为“鸡尾酒会效应”。
独立成分分析是从盲源分离技术发展而来的一种数据驱动的信号处理方法, 是基于高阶统计特性的分析方法。它利用统计原理进行计算,通过线性变换把数据或信号分离成统计独立的非高斯的信号源的线性组合。
主成分分析(PCA)是一种数据降维的方法,它与主成分分析有一些区别:
1. 主成分分析假设源信号间彼此非相关,独立成分分析假设源信号间彼此独立。
2. 主成分分析认为主元之间彼此正交,样本呈高斯分布;独立成分分析则不要求样本呈高斯分布。
鸡尾酒问题
主成分分析来源于经典的鸡尾酒宴会问题(cocktail party problem)。假设在party中有n个人,他们可以同时说话,我们也在房间中一些角落里共放置了n个声音接收器(Microphone)用来记录声音。宴会过后,我们从n个麦克风中得到了一组数据,i表示采样的时间顺序,也就是说共得到了m组采样,每一组采样都是n维的。我们的目标是单单从这m组采样数据中分辨出每个人说话的信号。
将问题细化一下,有n个信号源,每一维都是一个人的声音信号,每个人发出的声音信号独立。A是一个未知的混合矩阵(mixing matrix),用来组合叠加信号s,那么
的意义在上文解释过,这里的不是一个向量,是一个矩阵。其中每个列向量是,
麦克风和声音源的关系图如下:
与的关系图如下:
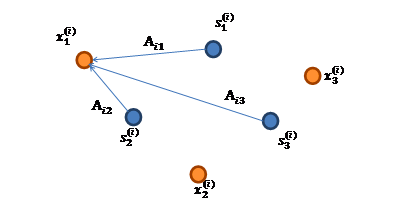 的每个分量都由的分量线性表示:
的每个分量都由的分量线性表示:
A和s都是未知的,x是已知的,我们要想办法根据x来推出s。这个过程也称作为盲信号分离。
令,那么
将 W 表示为:
其中,其实就是将写成行向量形式。那么得到:
ICA的不确定性:由于w和s都不确定,那么在没有先验知识的情况下,无法同时确定这两个相关参数。接下来将详细地讲解 ICA 的原理,解决 ICA 的不确定性问题。
数学原理
- 概率密度函数与累积分布函数
连续型随机变量的概率密度函数是一个描述这个随机变量的输出值在某个确定的取值点附近的可能性的函数。
累积分布函数是概率密度函数的积分,能完整描述一个实随机变量X的概率分布。对于所有实数x,累积分布函数定义如下:
即累积分布函数表示变量 X 小于某个值x时的概率。
F(X)与p(X)关系为:
对于,有
最后得到的结果是:
ICA算法
独立成分分析目标是实现在海量数据中学习完备的单位正交基,即从线性混合信号中恢复基本源信号。
a) ICA模型: (表示被观测信号由独立的源信号通过混合矩阵A混合而成)
b) 估计混合矩阵A和独立源信号s:假设条件
a) 成分是统计独立的
b) 独立成分是非高斯分布(高斯分布的独立等同于不相关,最多有且仅有一个高斯分布,即随机噪声)
c) 未知的混合矩阵A是方阵
d) 一般假设被观测到的信号数量不小于源信号的数量(噪声过大时,可作为独立源信号进行分析)估计方法
a) 非高斯最大化
- FastICA算法(负熵最大):该算法寻找方向使得随机变量的某种“非高斯性”的度量最大化。
- 四阶累积量(高阶积累量最大):类似PCA的流程,我们首先找使得最大;然后在与正交的空间里找,使得最大,以此类推直到找到所有的. 可以证明,用这种方法得到的是相互独立的。
b) 最大似然估计
c) 互信息最小化:Informax算法
ICA算法归功于Bell和Sejnowski,这里使用最大似然估计来解释算法。
目标函数部分
我们假定每个有概率密度,那么给定时刻原信号的联合分布就是
这个公式代表一个假设前提:每个人发出的声音信号各自独立。有了,我们可以求得:
左边是每个采样信号x(n维向量)的概率,右边是每个原信号概率的乘积的|W|倍。
前面提到过,如果没有先验知识,我们无法求得W和s。因此我们需要知道,我们打算选取一个概率密度函数赋给s,但是我们不能选取高斯分布的密度函数。在概率论里我们知道密度函数p(x)由累计分布函数(cdf)F(x)求导得到。F(x)要满足两个性质是:单调递增和在[0,1]。我们发现sigmoid函数很适合,定义域负无穷到正无穷,值域0到1,缓慢递增。我们假定s的累积分布函数符合sigmoid函数。
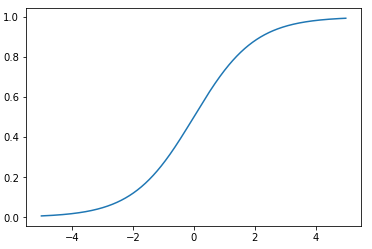
对求导得到:
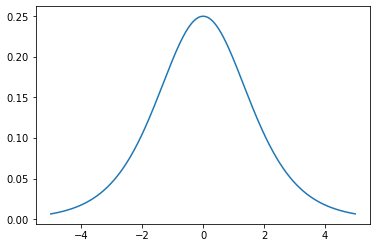
如果我们预先知道的分布函数,那就不用假设了;但是在缺失的情况下,sigmoid函数大多数情况下能够起到不错的效果。由于是个对称函数,所以均值,那么,x的均值也是0。知道了,就剩下W了。给定采样后的训练样本,使用前面得到的x的概率密度函数,样本对数似然估计如下: 大括号里面是.
优化部分(梯度下降算法)
接下来就是对W求导了,这里牵涉一个问题是对行列式|W|进行求导的方法,属于矩阵微积分:
最终得到的求导后公式如下, 的导数为 :
其中是梯度上升速率,是人为指定的。
当迭代求出W后,便可得到来还原出原始信号。
PCA和ICA对比
假设你观察到的信号是n维随机变量.主成分分析(PCA)和独立成分分析(ICA)的目的都是找到一个方向,即一个n维向量使得线性组合的某种特征最大化。
- PCA
PCA认为一个随机信号最有用的信息体包含在方差里。为此我们需要找到一个方向,使得随机信号x在该方向上的投影的方差最大化。接下来,我们在与正交的空间里到方向,使得的方差最大,以此类推直到找到所有的n个方向. 用这种方法我们最终可以得到一列不相关的随机变量:,且得到的随机变量的方差递减。
- ICA
ICA根据非高斯性最大化、最大似然估计、互信息最小化等方式来寻找相互独立的方向。假设噪声或不感兴趣的信号都比较微弱,PCA能根据数据的能量或方差把主要信号留下来。而ICA更智能——它不在意信号的能量或方差,只看独立性。所以给定的待分析的混合信号经任意的线性变换都不会影响ICA的输出结果,但会严重影响PCA的结果。
同时使用PCA 和 ICA解决鸡尾酒会问题
这是酒会上三个人各自产生的源信号:
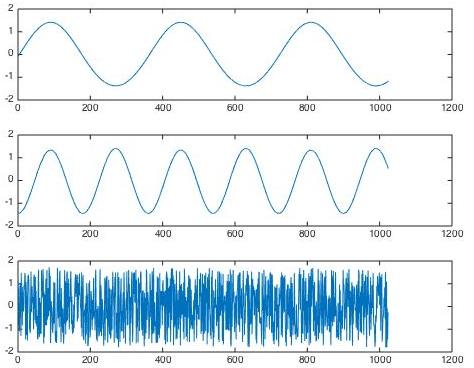
由6个麦克风分别随机录制这3个人产生的声音信号,则观测信号为:
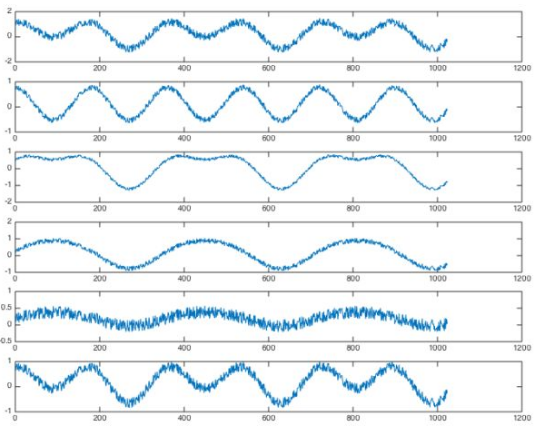
我们希望将他们分解开就需要用到ICA,但在ICA之前,往往会对数据有一个预处理过程,那就是PCA与白化。PCA本质上来说就是一个降维过程,大大降低ICA的计算量。PCA及白化后的结果如下图所示。可以看到,原先的6路信号减少为3路,ICA仅需要这3路混合信号即可还原源信号。
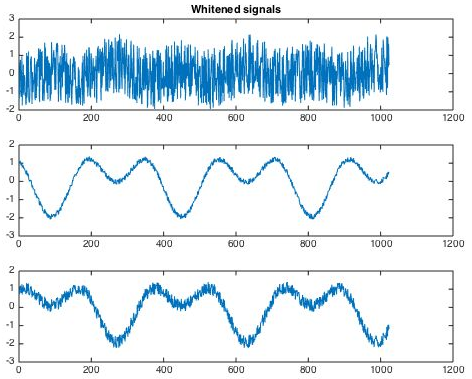
下面,ICA经过多步迭代寻优,就会按照信号之间独立最大的假设,将信号解混输出。
总的来说,ICA认为观测信号是若干个统计独立的分量的线性组合,ICA要做的是一个解混过程。而PCA是一个信息提取的过程,将原始数据降维,现已成为ICA将数据标准化的预处理步骤。
ICA的python实现
应用Python机器学习库SKlearn中的FastICA来演示信号分离并与PCA进行对比。
#coding:utf-8
import numpy as np
import matplotlib.pyplot as plt
from scipy import signal
from sklearn.decomposition import FastICA, PCA
# 生成观测模拟数据
np.random.seed(0)
n_samples = 2000
time = np.linspace(0, 8, n_samples)
s1 = np.sin(2 * time) # 信号源 1 : 正弦信号
s2 = np.sign(np.sin(3 * time)) # 信号源 2 : 方形信号
s3 = signal.sawtooth(2 * np.pi * time) # 信号源 3: 锯齿波信号
S = np.c_[s1, s2, s3]
S += 0.2 * np.random.normal(size=S.shape) # 增加噪音数据
S /= S.std(axis=0) # 标准化
# 混合数据
A = np.array([[1, 1, 1], [0.5, 2, 1.0], [1.5, 1.0, 2.0]]) # 混合矩阵
X = np.dot(S, A.T) # 生成观测信号源
# ICA模型
ica = FastICA(n_components=3)
S_ = ica.fit_transform(X) # 重构信号
A_ = ica.mixing_ # 获得估计混合后的矩阵
# PCA模型
pca = PCA(n_components=3)
H = pca.fit_transform(X) # 基于PCA的成分正交重构信号源
# 图形展示
plt.figure()
models = [X, S, S_, H]
names = ['Observations (mixed signal)',
'True Sources',
'ICA recovered signals',
'PCA recovered signals']
colors = ['red', 'steelblue', 'orange']
for ii, (model, name) in enumerate(zip(models, names), 1):
plt.subplot(4, 1, ii)
plt.title(name)
for sig, color in zip(model.T, colors):
plt.plot(sig, color=color)
plt.subplots_adjust(0, 0.1, 1.2, 1.5, 0.26, 0.46)
plt.show()
由结果可知,原始观测信号源有3种独立信号源混合(正弦、方形和锯齿波形),通过ICA可以较好的分离出三种信号源,而PCA的分离效果不佳,只分离出一个信号源。
from sklearn.decomposition import FastICA
ica = FastICA(n_components=None, algorithm='parallel', whiten=True, fun='logcosh', fun_args=None, max_iter=200, w_init=None)
以上是 FastICA 模型通常所含的参数及其对应的默认值。 n_components: 指定使用元素的数目。 algorithm: {'parallel','deflational'},指定 FastICA 使用哪种算法。 writen: True/False,是否进行白化处理。 fun: {'logcosh','exp','cube',..},选择一种近似于计算负熵的目标函数,可自己定义函数。 fun_args: 指定目标函数所要用的参数。 max_iter: 指定拟合过程中最大的迭代次数。 w_init: 指定初始的混合矩阵。
参考资料
- 特征哈希(Feature Hashing)
- Trevor Hastie et al. The Elements of Statistical Learning, 2001.
- Kilian Weinberger et al. Feature Hashing for Large Scale Multitask Learning, 2010.
- Joshua Attenberg et al. Collaborative Email-Spam Filtering with the Hashing-Trick, 2009.
- https://www.zhihu.com/question/264165760/answer/277634591
- sklearn.feature_extraction.FeatureHasher
- sklearn学习笔记2 Feature_extraction库
- 特征选择和稀疏学习
- 《西瓜书》笔记11:特征选择与稀疏表示(三)
- 特征选择与稀疏学习
- https://www.zhihu.com/question/24124122/answer/50403932
- https://blog.csdn.net/u014595019/article/details/52433754
- PCA算法详解
- 主成分分析(PCA)原理详解
- 主成分分析PCA算法:为什么去均值以后的高维矩阵乘以其协方差矩阵的特征向量矩阵就是“投影”?
- 用Python的sklearn库进行PCA(主成分分析)
- 用scikit-learn学习主成分分析(PCA)
- 独立成分分析(Independent Component Analysis)
- 独立成分分析 ( ICA ) 与主成分分析 ( PCA ) 的区别在哪里?
- 独立成分分析ICA系列4:ICA的最优估计方法综述
- ICA-独立成分分析
- 独立成分分析Independent component analysis(ICA)
- 线性判别分析LDA原理总结
- 一文读懂特征工程
- 线性判别分析LDA详解
- LinearDiscriminantAnalysis
- 用scikit-learn进行LDA降维
- https://blog.csdn.net/u010705209/article/details/53518772
- https://blog.csdn.net/u012162613/article/details/42214205
- https://blog.csdn.net/qianhen123/article/details/40077873
- https://github.com/ceys/jdml/wiki/ALS
- 美团点评技术团队之深入FFM原理与实践
- [深度学习笔记(一)稀疏自编码器] (https://blog.csdn.net/u010278305/article/details/46881443)
- Field-aware Factorization Machines for CTR Prediction ,Yuchin Juan et al.
- Factorization Machines, Steffen Rendle et al.[2010]
- http://deeplearning.stanford.edu/wiki/index.php/UFLDL_Tutorial
- 局部线性嵌入(LLE)原理总结
- Locally linear embedding(LLE)局部线性嵌入-降维
- LocallyLinearEmbedding
- 用scikit-learn研究局部线性嵌入(LLE)
- 聚类和降维的区别与联系
- 聚类算法
- 受限玻尔兹曼机(RBM)学习笔记
- 受限制玻尔兹曼机RBM原理简介
- 从SNE到t-SNE
- t-SNE完整笔记
- SNE降维与可视化
- 比PCA降维更高级 —— t-SNE聚类算法实现指南